Different Types Of Flow in Channels
The Types Of Flow in Channels can be classified into following types depending upon the change in the depth
of flow with respect to space and time.
Steady Flow and Unsteady Flow
Flow in a channel is said to be steady if the flow characteristics at any point do not change with time that is (∂V/∂t)= 0, (∂y/∂t) = 0 etc. However, in the case of prismatic channels the conditions of steady flow may be obtained if only the depth of flow does not change with time, that is (∂y/∂t) = 0. On the other hand if any of the flow characteristics changes with time the flow is unsteady. Most of the open channel problems involve the study of flow under steady conditions and therefore in this chapter only steady flow has been considered.
Uniform and Non-uniform (or Varied) Flow.
Flow in a channel is said to be uniform if the depth, slope, cross-section and velocity remain constant over a given length of the channel. Obviously, a uniform flow can occur only in a prismatic channel in which the flow will be uniform if only the depth of flow y is same at every section of the channel, that is (∂y/∂s) = 0.
Flow in channels is termed as non-uniform or varied if the depth of flow y, changes from section to section, along the length of the channel, that is (∂y/∂s) is not equal to zero. Varied flow may be further classified as rapidly varied flow (R.V.F.) and gradually varied flow (G.V.F.). If the depth of flow changes abruptly over a comparatively short distance, the flow is characterized as a rapidly varied flow. Typical examples of rapidly varied flow are hydraulic jump and hydraulic drop. In a gradually varied flow the change in the depth of flow takes place gradually in a long reach of the channel.
Laminar Flow and Turbulent Flow.
Just as in pipes, the flow in channels may also be characterized as laminar, turbulent or in a transitional state, depending on the relative effect of viscous and inertia forces and alike pipes, Reynolds number Re is a measure of this effect in channel flow also. However, the Reynolds number for flow in channel is commonly defined as
Re = 〈ρVR〉/u, where V is the mean velocity of flow, R is the hydraulic radius (or hydraulic mean depth) of the channel section
and ρ and μ are respectively the mass density and absolute viscosity of water.
On the basis of the experimental data it has been found that up to Re equal to 500 to 600 the flow in channels may be considered to be laminar and for Re greater than 2000 the flow in channels is turbulent. Thus for Re in between 500 to 2000 the flow in channels may be considered to be in transitional state. Since most of the channel flows are turbulent, in this chapter only the turbulent flow has been dealt with.
Subcritical Flow, Types Of Flow in Channels
Critical Flow and Supercritical Flow. As stated earlier gravity is a predominant force in the case of channel flow. As such depending on the relative effect of gravity and inertia forces the channel flow may be designated as subcritical, critical or supercritical.
The ratio of the inertia and the gravity forces is another dimensionless parameter called Froude number Fr which is defined as Fr = VgD ; where V is the mean velocity of flow, g is acceleration due to gravity and D is hydraulic depth of channel section (as defined in Section 15.3). As indicated later, when Fr = 1, that is V = gD , the channel flow is said to be in a critical state. If Fr < 1, or V < gD , the flow is described as subcritical or tranquil or streaming. If Fr >1, or V > gD , the flow is said to be supercritical or rapid or shooting or torrential.
GEOMETRICAL PROPERTIES OF CHANNEL SECTION
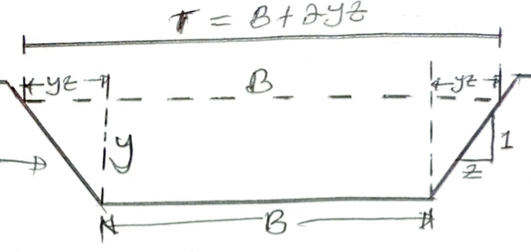
The geometrical properties of a channel section can be defined entirely by the geometry of the section and the depth of flow. Some of the geometrical properties of basic importance are defined below. The depth of flow y, is the vertical distance of the lowest point of a channel section from the free surface. The top width T is the width of the channel section at the free surface.
The wetted area A (or water area or area of flow section) is the cross-sectional area of the flow normal to the direction of flow. The wetted perimeter P is the length of the channel boundary in contact with the flowing water at any section.
The hydraulic radius R (or hydraulic mean depth) is the ratio of the wetted area to its wetted
perimeter, or R = A/P
The hydraulic depth D is the ratio of the wetted area to the top width T, or D = A/T
The section factor for critical flow computation Z is the product of the wetted area and the square root of the hydraulic depth, or
Z = A√D = A√A/T = 〈A3/T〉1/2
The section factor for uniform flow computation AR2/3 is the product of the wetted area and the
hydraulic radius to two-thirds power.
The table below provides a list of the expressions for the geometrical properties of five commonly used
channel sections.