The volume of irregular object computations.
Simpson’s rule
A = L/3[O1 + ON+ 4∑even offsets + 2∑remaining odd offsets]
Problem 3.
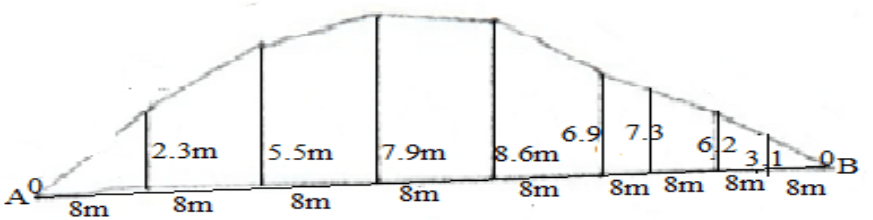
Consider the offsets measured from line AB to the irregular boundary as
given in the table below respectively. Calculate the area contained between
line AB and the irregular boundary using Simpson’s rule, with an even number of offsets.
| Length (m) | 0A | 8 | 16 | 24 | 32 | 40 | 48 | 50 | 64 | 72B |
| Offset (m) | 0 | 2.3 | 5.5 | 7.9 | 8.6 | 6.9 | 7.3 | 6.2 | 3.0 | 0 |
Solution:
Here, we calculate the area between offset 1 to 9 by Simpson’s rule and the
area between offset 9 to10 by trapezoidal rule.
Area = L/3[O1 + ON+ 4∑even offsets + 2∑remaining odd offsets]
Thus:
A1-9= 8/3[0 + 3.1 + 4(2.3 + 7.9 + 6.9 + 6.2) + 2(5.5 + 8.6 + 7.3)] =
370.9m2
A9-10 = 8/2[3.1 +0] = 12.4m2
Therefore: Total area, A, is given by:
A = A1-9 + A9-10=370.9+ 12.4 = 383.3m2