Table of Contents
ToggleENGINEERING SURVEY I $ II
Recommend a friend a friend a friend
Problem 05 solved, Computation of area volumes.
Computation of area volumes. Problem 05 (A) The Following Offsets Were Taken from A Chain Line to An Irregular Boundary Line at an Interval Of 10 M.: 3.10, 4.20, 5.35, 6.45, 7.15, 8.25, 7.95, and 5.20m. Compute the area between the chain line, the irregular boundary line, and the end offsets by Trapezoidal rule Simpson’s rule (B) The table below gives the lengths and the bearing of the lines of a traverse ABCDE, the length and bearing of EA having been omitted. Line Length (m) Bearing AB 204 87°30′ BC 226 20°20′ CD 187 280°00′ DE 192 210°00′ EA ? ? Calculated the length and bearing of the line EA. Solutions. (A) Given offsets, 3.10, 4.20, 5.35, 6.45, 7.25, 8.25, 7.95, 5.20. the values can be written in form of yo, y1, y2, y3 … yn. Hence the distance, h = 10m By trapezoidal rule, Computation of area volumes. Area = (h / 2) [ (y0+ yn ) + 2(y1+y2+y3+…..+yn−1)] = (10/2) ( (3.1+5.2) + 2(4.2+5.35+6.45+7.15+8.25+7.95)) = 435 m2. By Simpson’s rule Computation of area volumes. Area = (h / 3) x [ (y1+ yn ) + 4(y2+y4+ ….. yn-2) + 2 x (y3 + y5 + y7 + … yn-1)] = (10/3) x ((3.1+5.2) + 4 x (4.2 + 6.45+ 8.25) + 2 x (5.35+ 7.15+ 7.95)) = 416 m2. (B) For a correct closed traverse, there are some checks. ∑ Latitude = 0. ∑ Departure = 0. Latitude = L x Cosθ . Departure = L x Sin θ θ is the magnetic bearing of line. ∑ Latitude = (204 x Sin 87,30) +( 226 x Sin 20,20) +( 187 x Sin 280) + (192 x Sin 210,30) + (L x Sin θ) = 0 => L x Sinθ = -98.371 ∑ Departure = (204 x Cos 87,30) +( 226 * Cos 20,20) +( 187 * Cos 280) + (192 x Cos 210,30) + (L x Cos θ) = 0 => L Cos θ = – 87.855 (L Sin θ / L cos θ) = 1.119 => Tan θ = 1.119 => θ = Tan-1 (1.119) = 48.214 degrees. or (180+48.214) =228.214 degrees. Because Lsinθ is negative L = – 98.371 / Sin 228.214 = 131.928m => L = 131.928m. Computation of area volumes.

Problem 04 solved, Volume of area computations.
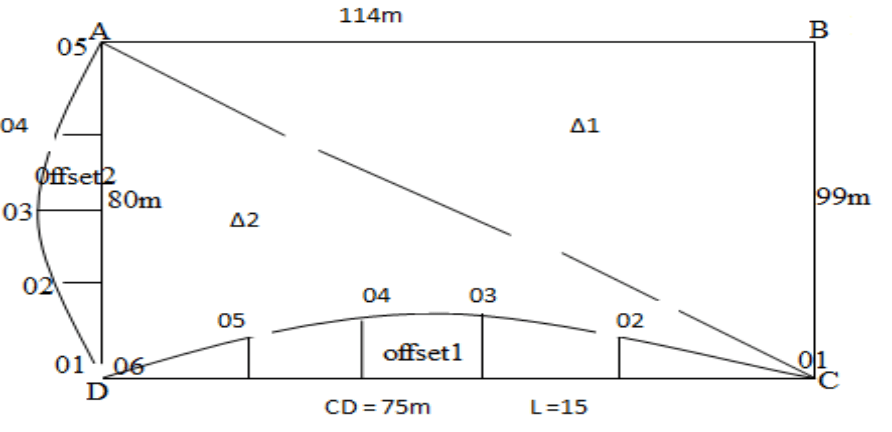
Volume of area computations. Problem 4. A, B, C, and D are the four clockwise considered boundary points of a plot. Sides AB and BC are straight, while sides CD and DA are irregular, with < CBA = 900, A straight line CD does not cross the plot, while a straight line DA passes inside the plot. Other measurements along the straights are as follows: AB = 114m, BC = 99m, with line AC not crossing any boundary. The offsets measured from lines CD and DA to irregular boundaries are given in Tables I & II respectively. Chainages (m) 0 (C) 15 30 45 60 75D Offsets (m) 0 1.8 2.8 3.88 1.9 0 Chainages (m) 0 (D) 20 40 60 80 (D) Offsets (m) 0 1.02 3.05 1.22 0 Calculate the area of the plot in hectares, applying Simpsons and Trapezoidal rules in tables I & II respectively. Solutions: Using Simpson’s rule (Volume of area computations.) Area of plot = area of ∆1 + area of ∆2 – Offset area1 + Offset area2 Area of ∆1 = ½ bh = ½ x 114 x99 = 5643m2 Area of ∆2 = √S (S-a) (S-c) (S-d) AC = √ (AB2 + BC2) = √ (1142 + 992) = 150.99m Where: S = (a + c + d)/2 S = (75 + 80 + 150 .99)/2 = 152.99m Area of ∆2 = √152.99(152.99- 75) (152.99-80) (152.99- 150.99) =1319.77m2 Offset Area1 i.e., Tables 1 by Simpsons rule but offsets are even. So, we shall use Simpsons rule for A1-5 & then Trapezoidal for A5-6 A = L/3 [01 + 0N + 4∑even offset + 2∑odd offsets] A1-5 = L/3 [(01 + 05 + 4 (02 + 04) + 2 (03)] A1-5 = 15/3 [0 + 1.95 + 4 (1.8 +3.88) + 2(2.8)] = 151.35m2 Using trapezoidal rule. (Volume of area computations.) A5-6 = L/2 (06 + 05) = ½ (0 + 1.95) x15 = 14.63m2 Offset area 1 = 151.35 +14.6 3 = 165.98m2 Offset area 2 i.e., table II by Trapezoidal rule. A = L/2 [(01 + 0N + 2 (02 + 03 + ……..+ 0N-1)] = 20/2 [0 + 0 + 2 (1.02 + 3.05 + 1.22)] = 105.8m2 Total Area of the plot = 5643 + 1319.77 – 165.98 + 105.80 = 6902.59m2 = 0.6902hect. Volume of area computations.
Problem 03 Solved, Volume of irregular object computations.
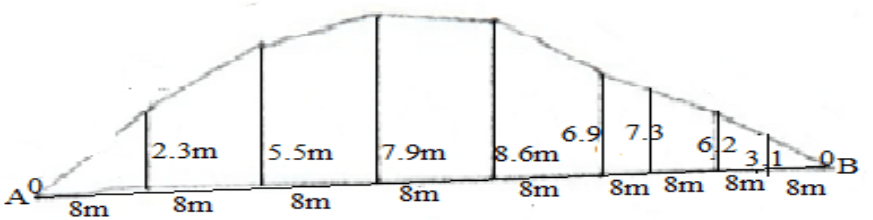
The volume of irregular object computations. Simpson’s rule A = L/3[O1 + ON+ 4∑even offsets + 2∑remaining odd offsets] Problem 3. Consider the offsets measured from line AB to the irregular boundary as given in the table below respectively. Calculate the area contained between line AB and the irregular boundary using Simpson’s rule, with an even number of offsets. Length (m) 0A 8 16 24 32 40 48 50 64 72B Offset (m) 0 2.3 5.5 7.9 8.6 6.9 7.3 6.2 3.0 0 Solution: Here, we calculate the area between offset 1 to 9 by Simpson’s rule and the area between offset 9 to10 by trapezoidal rule. Area = L/3[O1 + ON+ 4∑even offsets + 2∑remaining odd offsets] Thus: A1-9= 8/3[0 + 3.1 + 4(2.3 + 7.9 + 6.9 + 6.2) + 2(5.5 + 8.6 + 7.3)] = 370.9m2 A9-10 = 8/2[3.1 +0] = 12.4m2 Therefore: Total area, A, is given by: A = A1-9 + A9-10=370.9+ 12.4 = 383.3m2 Volume of irregular object computations.

Problem 02 Solved, Volume of irregular object computations.
The volume of irregular object computations. Trapezoidal rule A = L/2[01, + ON+ 2(02 + O3 + O4 +……+ ON-1)]…………………….. (i) Problem 2 The following, offsets 8m apart, were measured at right angles from a traverse line to an irregular Boundary. 0 m, 2.3 m, 5.5 m, 7.9 m, 8.6 m, 6.9 m, 7.3 m, 6.2 m, 3.1 m, and O m. Calculate the area between the traverse line and the irregular boundary. Solution: From the general trapezoidal rule, area is given by. A = L/2[01 + O10+ 2(02 + O3 + O4 +05 +06 +07 +08+ O9)] In this case L = 8m. Thus: A = 8/2[0 + 0 + 2(2.3 + 5.5 + 7.9 + 8.6 + 6.9 + 7.3+ 6.2 + 3.1)] = 4[2(47.8)] = 382.4m2 volume of irregular object computations.
Problem solved; A theodolite whose constants are K= 100 and C=0
A theodolite Stations M, N, and P are for a right-angled triangle at station M as shown below. A theodolite whose constants are K= 100 and C=0 was used to determine the following chemometric data. Instrument station M Height of instrument I 1.410m The reduced level of the station is 129.600m Target station Vertical angle Stadia hair readings lower middle upper N -5040/ 1.170 1.500 1.830 P 2030/ 2.410 2.610 2.810 Calculate: (a). Horizontal length MN and MP (b). Horizontal length NP (c). Reduced level of N and P (d). Slope between p and N in form of 1 in n Solution: (a). Horizontal length MN (HMN) HMN = CSCos2θ + KCosθ where C=100, S = 1.830-1.170 = 0.660m k = 0 HMN =100x 0.66Cos25040` = 65.36m Horizontal length MP (HMp) HMp = CSCos2θ + KCosθ where C=100, S = 2.810-2.410 =0.400m HMp =100x 0.40Cos22030` = 39.92m (b). Horizontal length NP =√ ( MN2 + MP2) =√ (65.362 + 39.922) = 76.59m ( c ). Reduced level at N Using RLs = RLI + i ±V-M RLN = RLm + I ±V-m, Where RLm = 129.600m, I = 1.410m M = 1.500m V= ½(CSSin2θ) + ksinθ =1/2x 100×0.66Sin2(-5040`) = -6.49m Therefore, the Reduced level at N = 129.60 + 1.41 – 6.49- 1.5 = 123.020m Reduced level at P =RLm + I ±V-m Where RLm = 129.600m I = 1.410m M = 2.610m V= ½(CSSin2θ) =1/2x 100×0.40Sin2(2030= 1.743m Therefore, the Reduced level at P = 129.60 + 1.41 +1.743- 2.610 =130.143m (d). Slope between p and N in form of 1 in n Slope =∆y/∆x = (7.123)/(76.59) = 0.093 = 1in n = 1in10.75 A theodolite

Problem 2.18 Reciprocal leveling involving a single. solved
2.18 Reciprocal leveling involving.. single level was used to transfer height. across a river between two points R1 and R2 70 m apart. Using the following readings, calculate the height change from R1 to R2 and the collimation error in the level. Level set up close to R1: Staff reading on R1 = 1.582 m Staff reading on R2 = 0.792 m Level set up close to R2: Staff reading on R1 = 2.112 m Staff reading on R2 = 1.336 m Expert Answer ♥♥♥ 2.18 Reciprocal leveling involving.. Solved.
problem 2.17 The extract given below is for levels taken.. solved
The extract given below is for levels taken.. between two TBM, calculate the adjusted reduced levels for all the entries in the book. Arithmetic check ΣBS – ΣFS = Last RL – First RL 7.719 – 9.031 = 30.005 – 31.317 – 1.312 = – 1.312 ok. Since Last RL given = 30.005, therefore a correction is needed. Correction per step = 30.007 – 30.005/6 Correction = 0.000333m extract given below is for levels taken .. Solved.
Problem 2.15 For the leveling shown below, calc .. Solved,
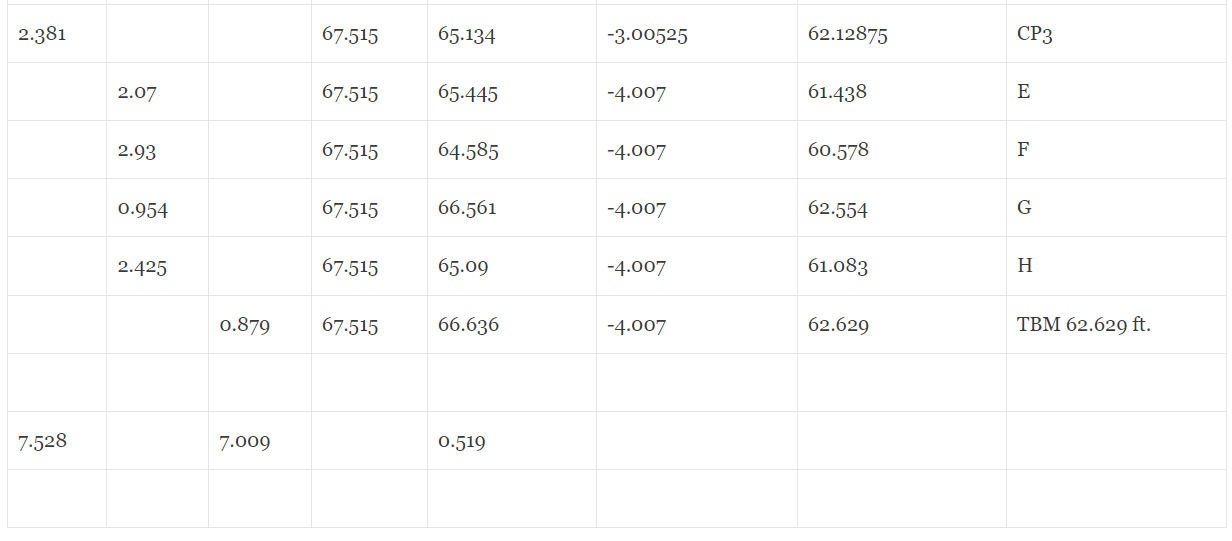
2.15 For the leveling shown.. 2.15 For the leveling shown below, calculate adjusted reduced levels for all points in the level table Expert Answer ♥♥♥ ANSWER 2.15 For all station, HPC = known Reduced Level + Backside Reduced level/RL = HPC – (IS or FS) Now, for calculation Checks, (Sum of all backside/BS) – (Sum of all Foreside/FS) = (Last reduced level/RL) – (First reduced level/RL) = 7.528 – 7.009 = 66.636 – 66.117 = 0.519 For correction Net Correction = Actual final RL – Calculated final RL = 62.629 – 66.636 = -4.007 Number of stages = No of BS = No of FS = 4 in this case There4, correction = = = -1.00175 Correction in stage one (red) = 1 X Correction = -1.00175 // // two (green)= 2 X Correction = -2.0035 // // three (yellow) = 3 X Correction = -3.00525 // // Four (blue) = 4 X Correction = -4.007 For all Reduced Levels, Corrected RL = Calculated RL + Correction 2.15 For the leveling shown .. solved.
2.13, A digital level was checked for collimation error using …Solved
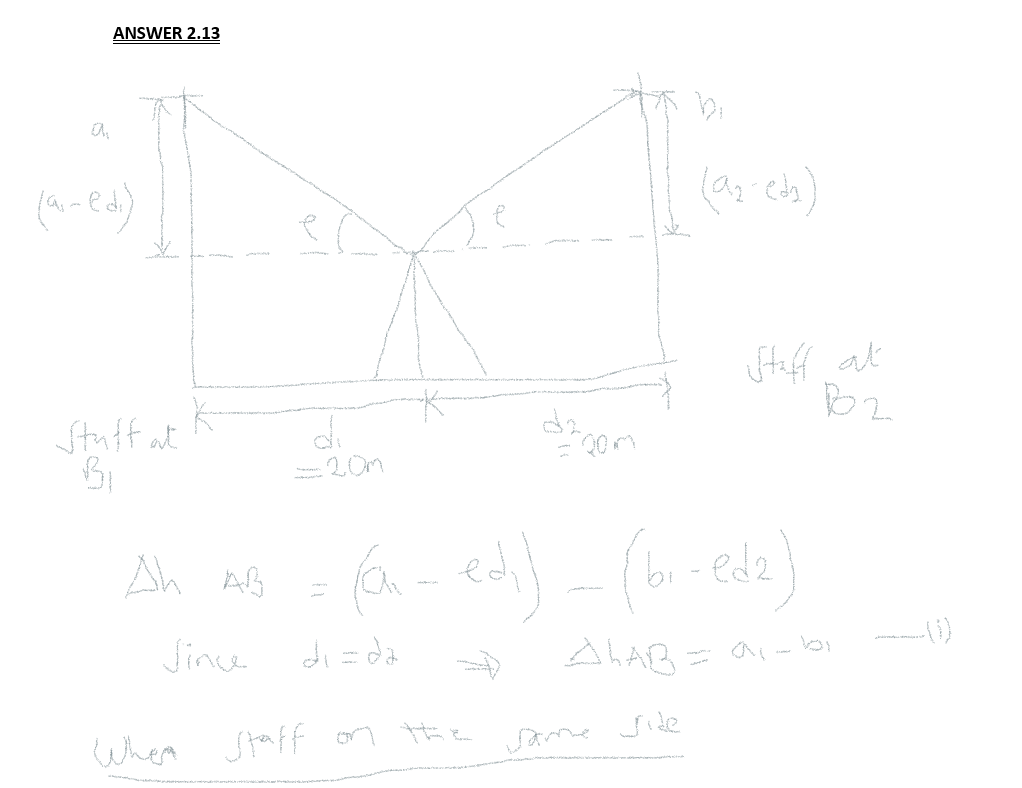
2.13, A digital level was checked for collimation error using a two-peg test and the following results were obtained. With the level midway between two pegs B1 and B2 which are 40 m apart: Staff reading at B1 = 1.476 m Staff reading at B2 = 1.432 m Level set up 10 m from B2 along the line B1–B2 extended: Staff reading at B1 = 1.556 m Staff reading at B2 = 1.472 m Calculate the collimation error in the level and the readings that would have been obtained with the level in the second position close to B2 had it has been in perfect adjustment. Expert Answer.♥♥♥ A digital level was checked.. answered.
