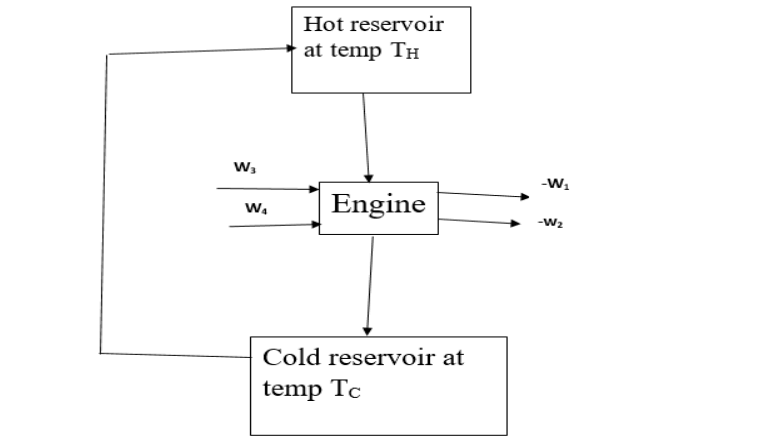
A Carnot engine
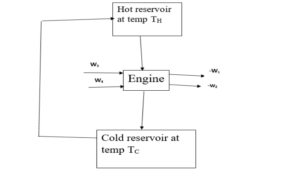
A Carnot engine problem.
Question two
(a) An engine that operates between the temperatures TH = 850K and TC = 300 K performs 1200 J of work per cycle;
(i) What is the efficiency of this engine? [4 marks]
Efficiency
TC = 300K
TH = 850K
W = 1200J
Eff = TH -TC/TH = 850 – 300/850
Eff = 0.647 = 64.7%
(ii) How much heat is extracted from the hot reservoir? [3 marks]
Amount of Heat.
Eff = W/QH
0.647 = 1200/QH
QH = 1854.7J
(b) If a Carnot engine operates with efficiency of 40 %. How much must the temperature of the hot reservoir increase, so that the efficiency increases to 60 %? The temperature of the cold reservoir remains at 9 0C.
Eff = 40%
Increase = 60%
TC = 9°C ⇒ 282K(Rankine)
TH1 = ?
Eff = TH1 – TC/TH1
0.4 = TH1 – 282/TH1
TH1 – 0.4TH1 = 282
0.6TH1 = 282
TH1 = 470K
Efficiency at 60% = 0.6
TC = 9°C ⇒ 282K(Rankine)
Eff = TH2 -TC/TH2
0.6 = TH2 -282/TH2
0.6TH2 = TH2 – 282
TH2-0.6TH2 = 282
0.4TH2 = 282
TH2 = 705K
TH = TH2– TH1 ⇒ 705 – 470
TH = 235K
Watch Carnot cycle operation, video by earthpen.